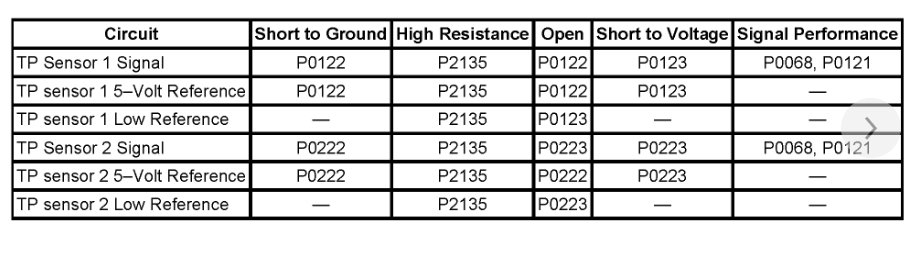
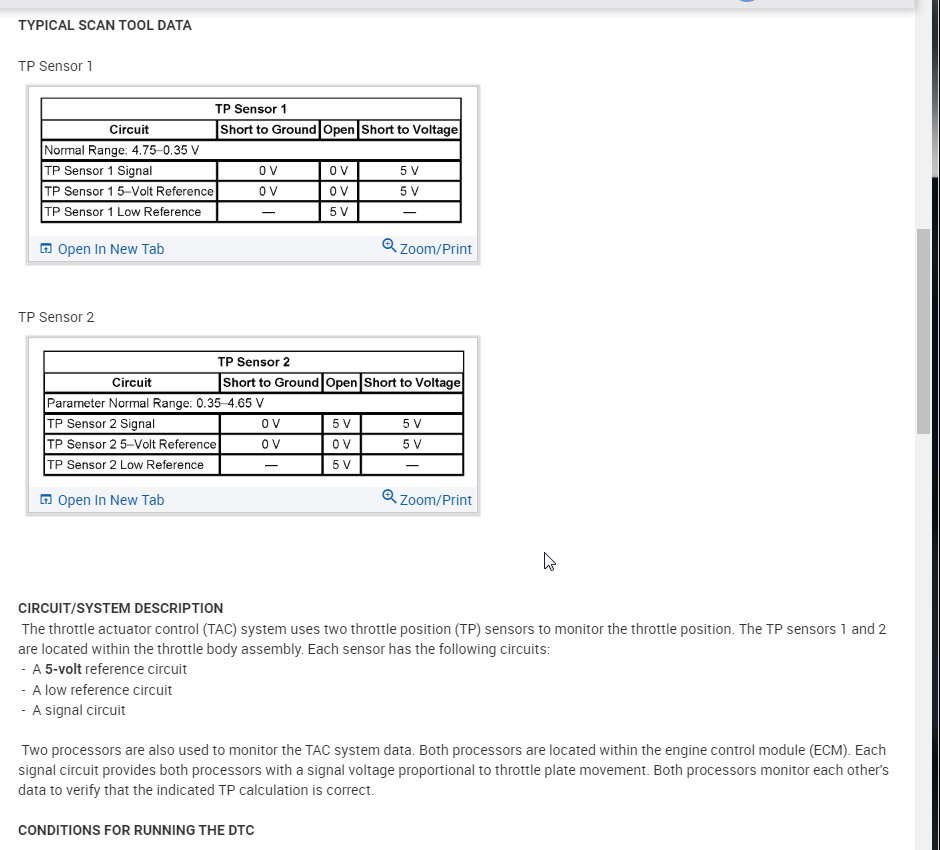
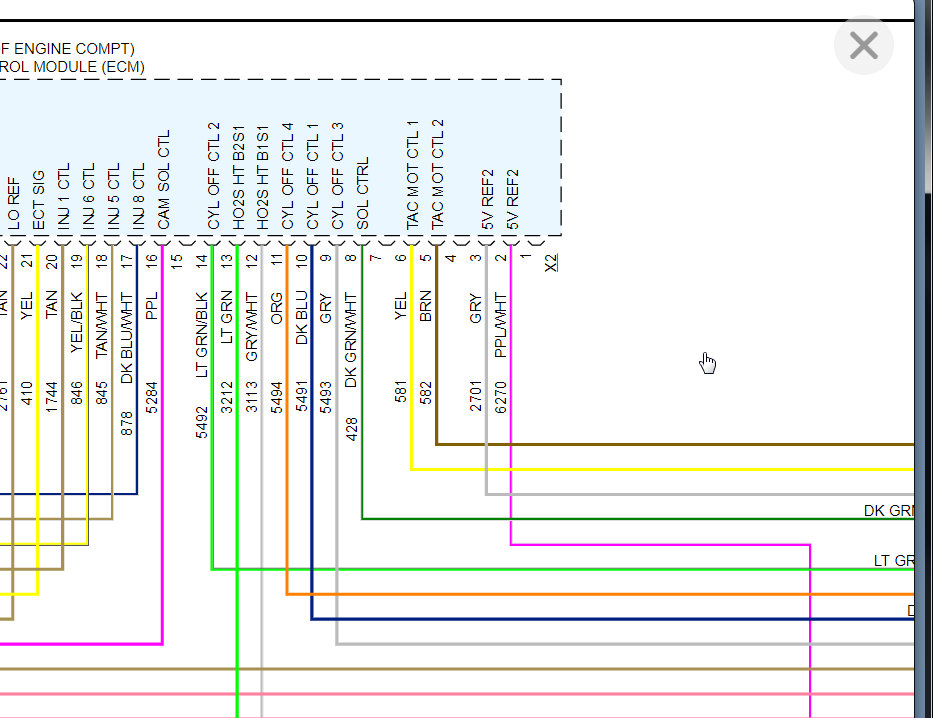
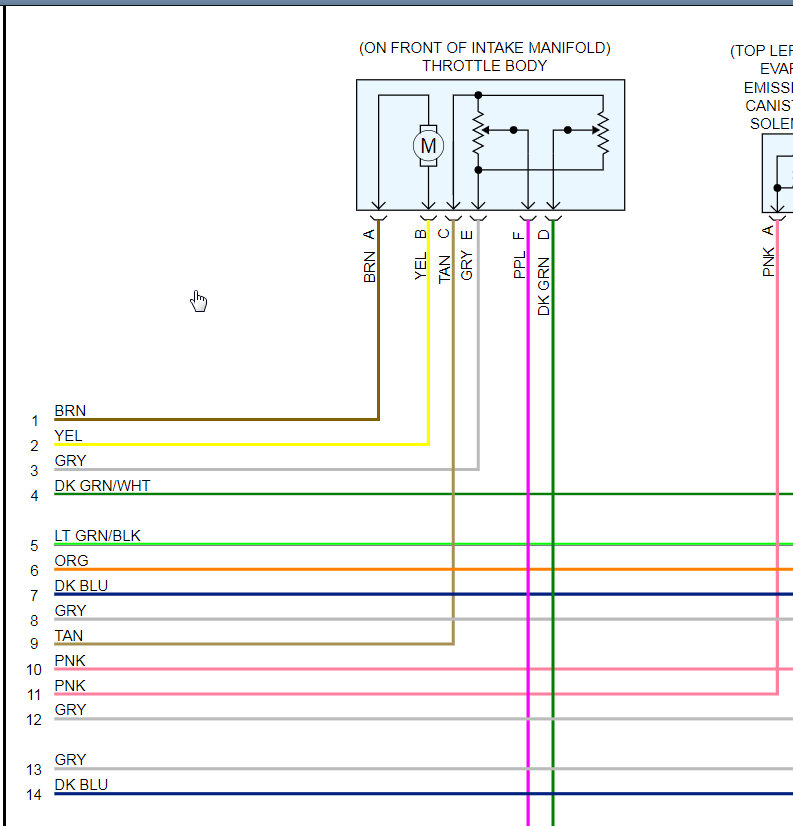
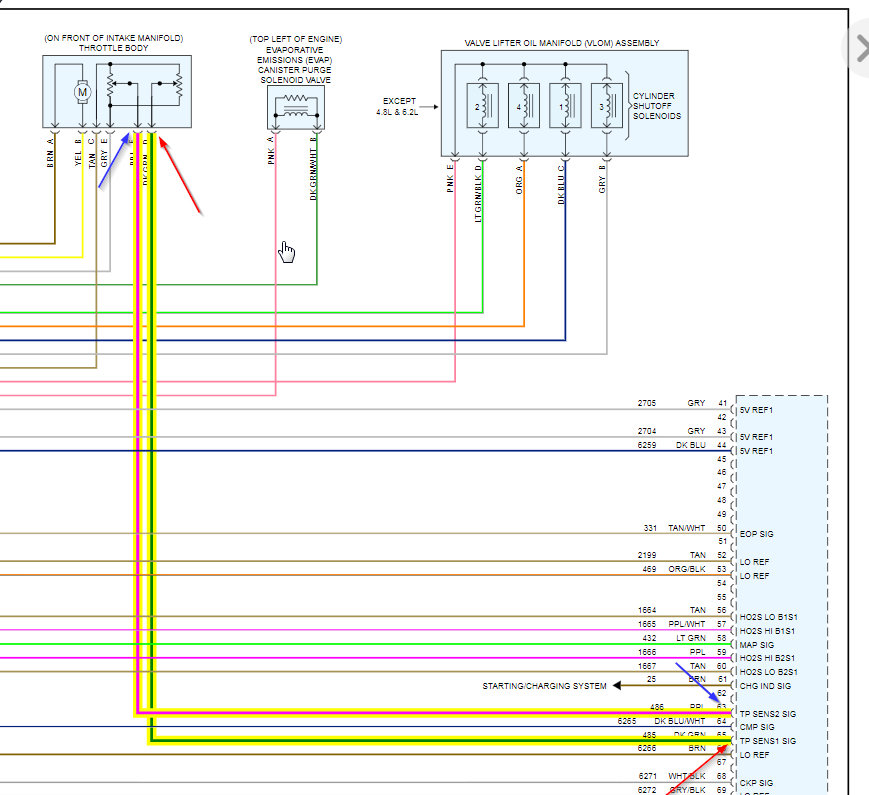
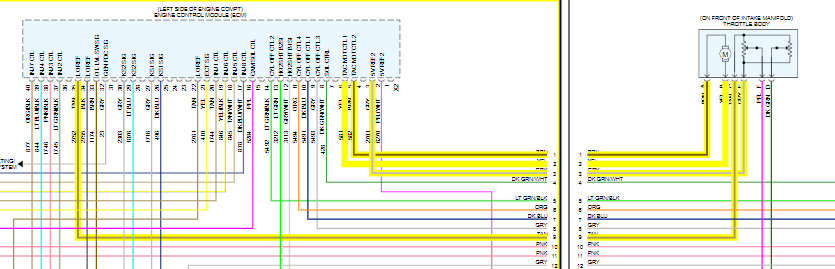
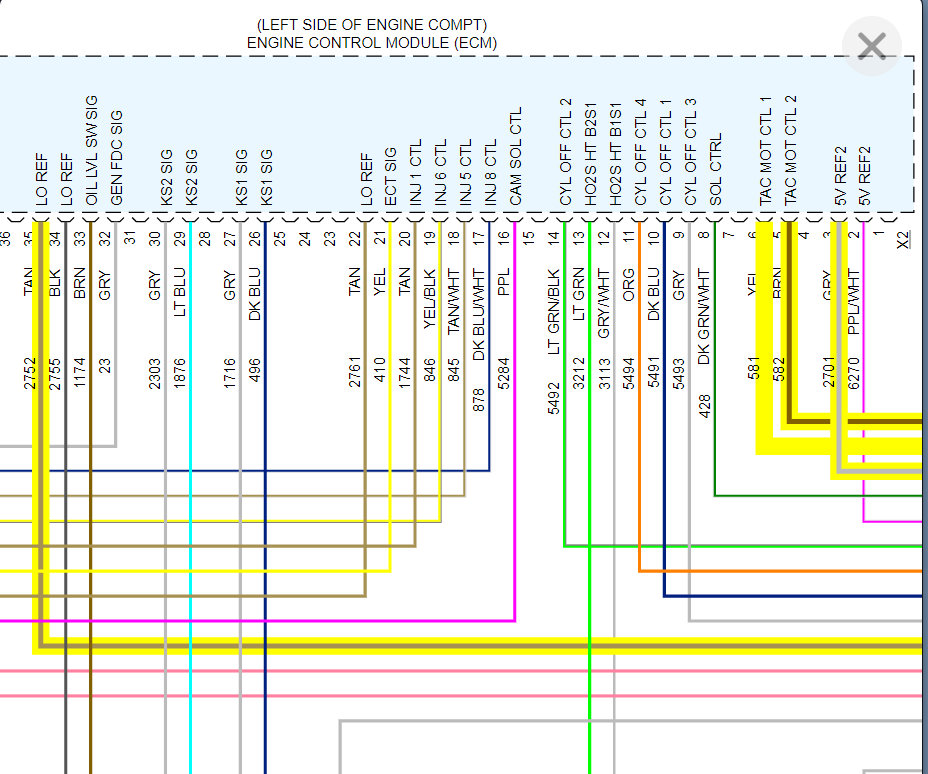
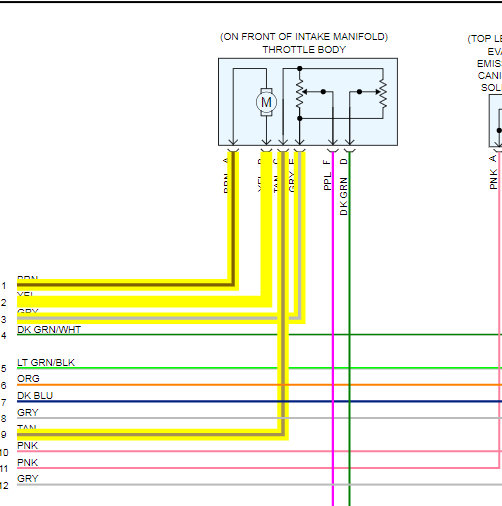
Monday, November 4th, 2019 AT 12:38 PM
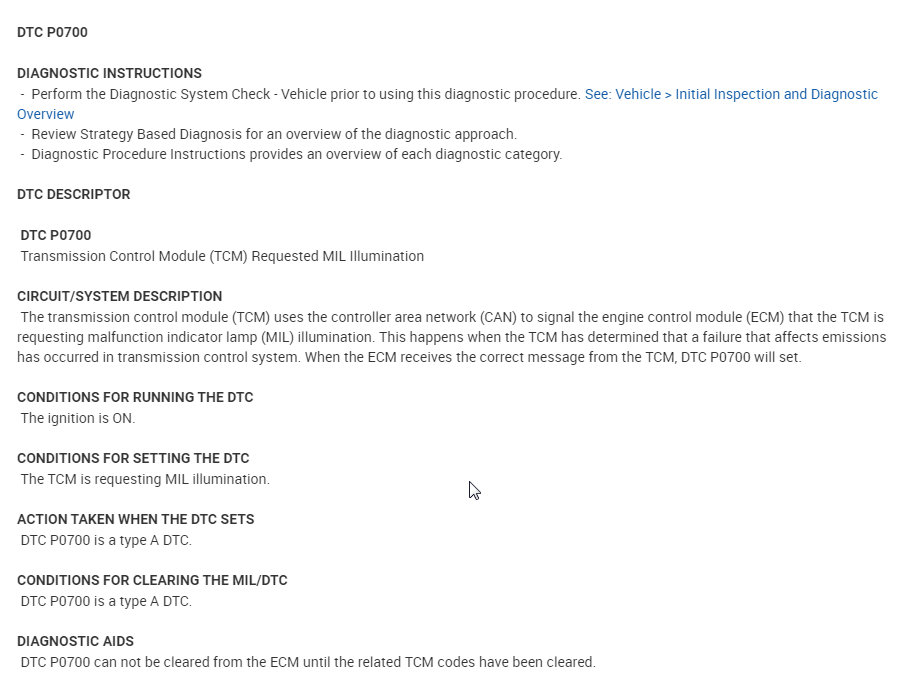
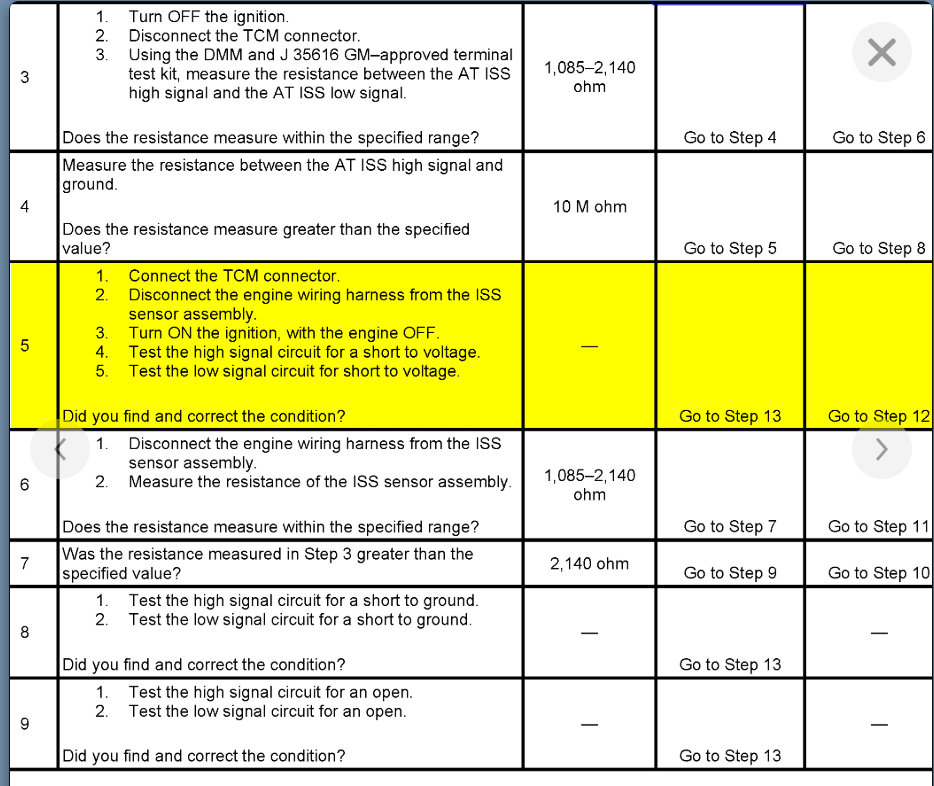
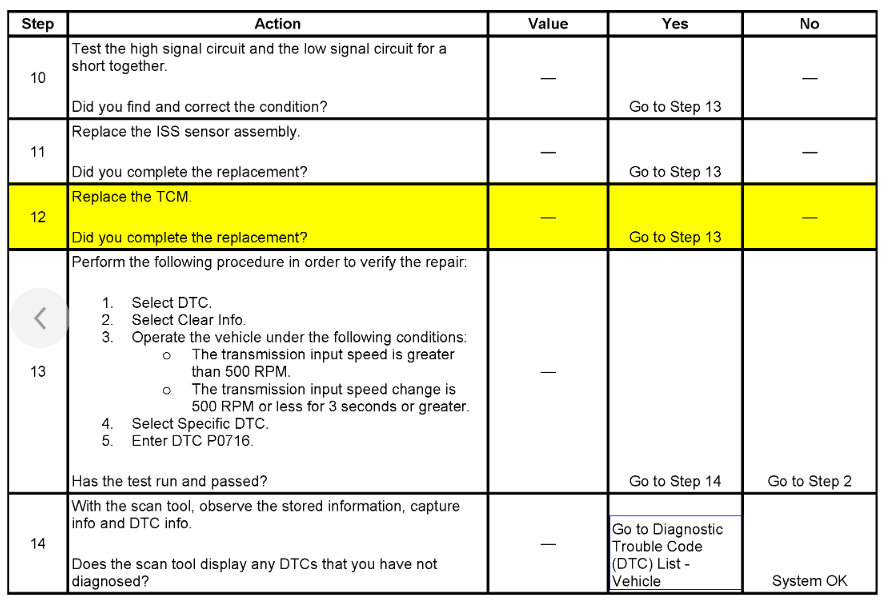
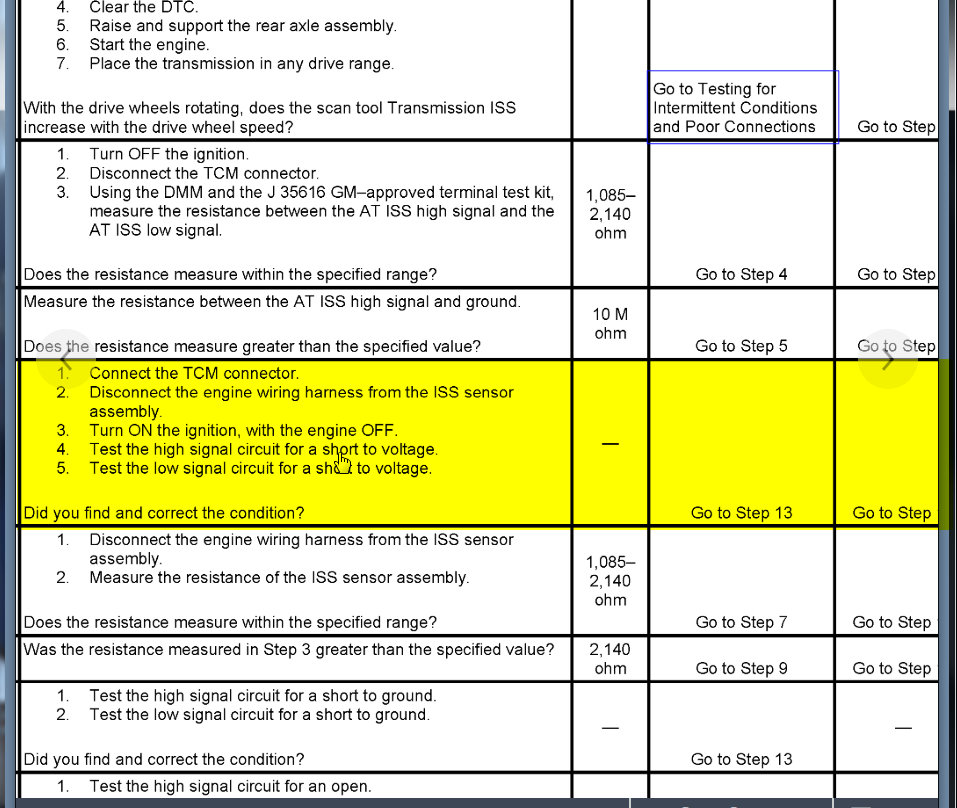
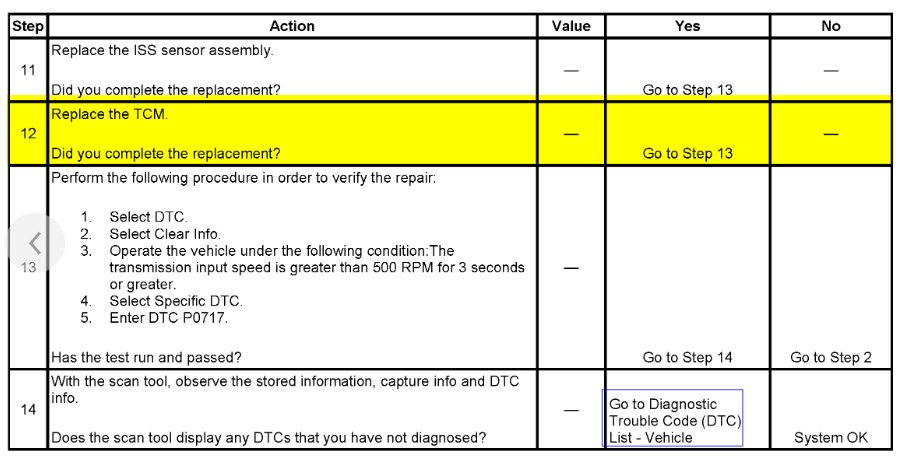
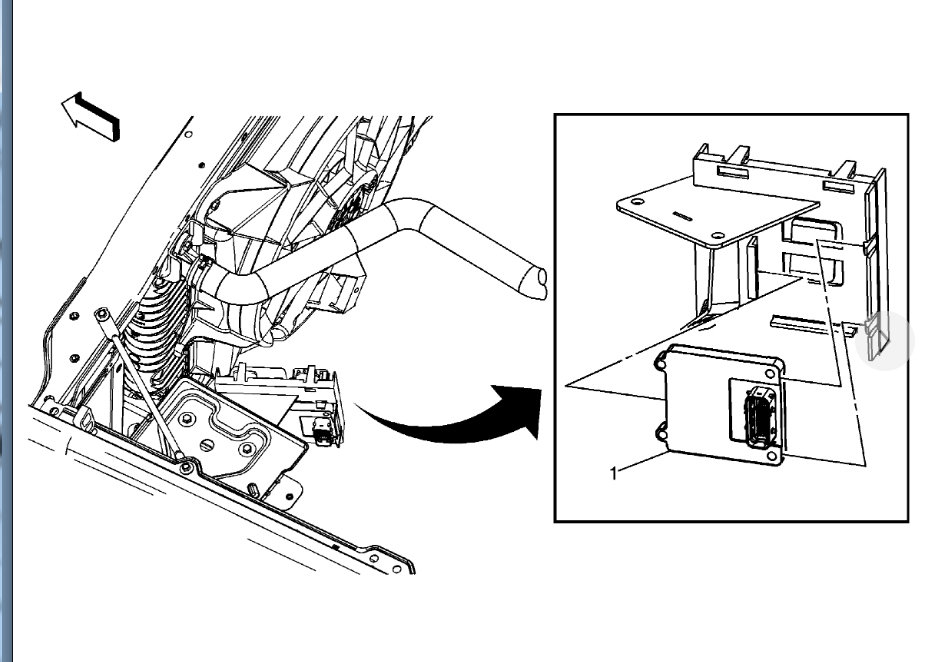
Yea, my check engine light came back on. I have not gone to get the codes checked, but every time I get them checked it is the same codes; P0700, P0716, and P0717 and I have replaced all of the sensors. Previously I have replaced the throttle body with sensor, the transmission input sensor, and I replaced the gas pedal with sensor and I also replaced the connectors to the sensors in case of wiring going bad. I unplug the battery when I work on it, so the codes clear and it drives better for a short amount of time but then starts shifting hard again and throws the same codes. So I'm thinking at this point it would be the transmission control module?