Will replacing stock rims with low profile rims damage the suspension?

This will not damage your suspension at all. However, the question of a leveling kit is a good one. You may need this in order to get full turning radius. The way to figure this out is calculate the circumference of the stock and replacement tires and they need to be pretty close. Since this is a truck you will have a little more clearance then a car but not a ton. So if you want to provide the actual tire size that will put on the vehicle we can calculate that for you.

https://www.2carpros.com/articles/wheel-removal-and-re-installation

Let us know. Thanks

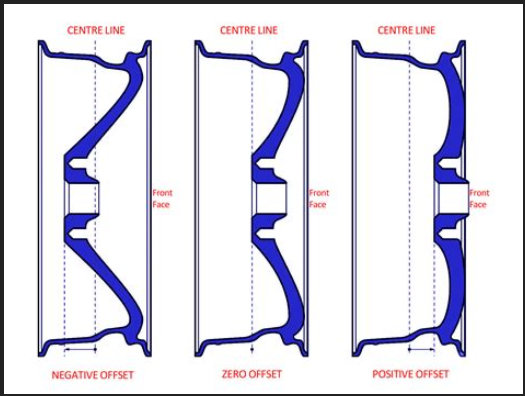
Okay, two things. First, since you already have the wheels and tires, are you sure the bolt pattern is correct and the correct offset? I attached a diagram below that will help with this.

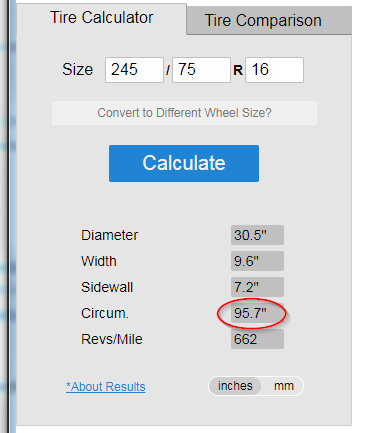
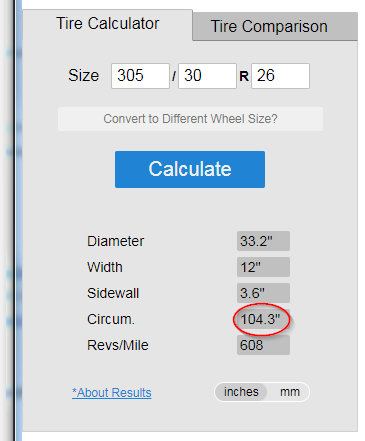
Second, the difference in circumference may be a little too much to leave it as stock. The difference is about 8 and a half inches. This means it is 4 inches on both sides.

So I would start with bolting them on the truck and checking the clearance in the wheel well area. If the tire is close to the fender liner then you are going to have to lift the truck. Then turn the wheel lock to lock and see if the tire touches the fender or frame rail. If it does then you are going to have to use a spacer as well.

Let me know if you have questions on this.

Wheels and tires will not damage your suspension. I am not sure what they are referring too but even if they are rubbing then they will really only hurt the wheel/tire.

So if they were on before and did not rub then I would say they are fine.

Again, I am not sure what they are talking about and how it would damage the suspension so if you can ask them again to give a little more detail on how this would happen, that may help me explain what they are talking about. Thanks

Sounds great. Thanks for the update. Please come back next time you need some help and thanks for using 2CarPros.