2004 LS transmission/tire sizes

Tiny
MARKSCOTT85
  • MEMBER
  • 2004 LINCOLN LS
  • V8
  • FWD
  • AUTOMATIC
  • 79,000 MILES
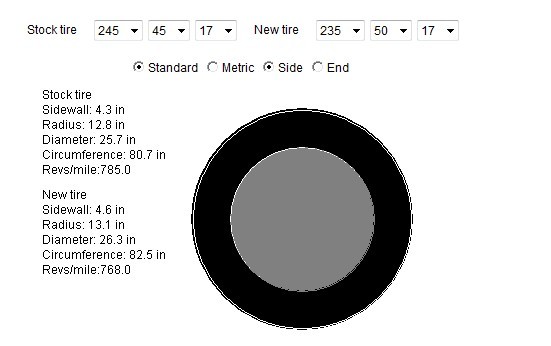
I have a 2004 LS. I just got the transmission replaced. The dealership said that it was because of the tires that were on the car, P245/45R17. When I called the dealership, I bought the car from they said the tires were fine. The standard tires for the car are P235/50R17.
Thursday, May 26th, 2011 AT 6:23 AM

11 Replies

Tiny
MARKSCOTT85
  • MEMBER
  • 3 POSTS
Car is rear wheel drive. Sorry.
Was this
answer
helpful?
Yes
No
Thursday, May 26th, 2011 AT 8:20 AM
Tiny
MERLIN2021
  • MECHANIC
  • 17,250 POSTS
Oversized tires can ruin steering parts, not usually transmissions, yours were an inch wider, I don't think that would do it.
Was this
answer
helpful?
Yes
No
Thursday, May 26th, 2011 AT 10:10 AM
Tiny
WRENCHTECH
  • MECHANIC
  • 20,761 POSTS
I agree with the dealer. Those tires were considerably taller, dramatically increasing the gear ratio and putting excessive strain and heat on the transmission that it wasn't engineered to take.
Was this
answer
helpful?
Yes
No
Thursday, May 26th, 2011 AT 11:06 AM
Tiny
MARKSCOTT85
  • MEMBER
  • 3 POSTS
I drive this car about 400 miles a month. If I wait a few weeks, is that likely to be a long-term issue?
Was this
answer
helpful?
Yes
No
Friday, May 27th, 2011 AT 10:35 AM
Tiny
WRENCHTECH
  • MECHANIC
  • 20,761 POSTS
You already lost one transmission because of this and it will void any warranty you have so why would you even ask that.
Was this
answer
helpful?
Yes
No
Friday, May 27th, 2011 AT 12:21 PM
Tiny
MERLIN2021
  • MECHANIC
  • 17,250 POSTS
I just checked tire chart and the difference between 235 and 245 goes from 26.25 to 26.65 I don't think iys enough to ruin a transmisson and 50 r to 45 r is width
Was this
answer
helpful?
Yes
No
Saturday, May 28th, 2011 AT 1:31 AM
Tiny
MERLIN2021
  • MECHANIC
  • 17,250 POSTS
P235/50r 17 is 26.25 high and 9.25 wide.
P245/45r is 25.68 high and 9.65 wide. 1/2 inch difference I would be shocked if that can ruin the tranny.
Was this
answer
helpful?
Yes
No
Saturday, May 28th, 2011 AT 1:39 AM
Tiny
WRENCHTECH
  • MECHANIC
  • 20,761 POSTS
No, that is incorrect. The 50 to 45 is an aspect ratio. When the aspect ratio is increases, so is the height and that would be in addition to the 10mm increase in cross section. There is nearly 2 inches difference in circumference between those 2 sizes
Image (Click to make bigger)
Thumb
Was this
answer
helpful?
Yes
No
Saturday, May 28th, 2011 AT 1:41 AM
Tiny
MERLIN2021
  • MECHANIC
  • 17,250 POSTS
Man that was fast! Are you alarmed? I will look into it again, but my chart shows what I posted. Again thanks for keeping abrest of this post
I could be misinformed.
I used an android app called garage buddy and rechecked it it does show the numbers I posted, it could be wrong, but since you were eaiti g to spring you findings on me instead of just posting them, I am curious!
Was this
answer
helpful?
Yes
No
Saturday, May 28th, 2011 AT 2:02 AM
Tiny
WRENCHTECH
  • MECHANIC
  • 20,761 POSTS
I was responding to your first post and hadn't seen the second one. Your numbers are not all that different from mine, I just have some additional info. The height isn't the real problem. It's the additional circumference that the height causes. We aren't talking about large amounts but some transmissions are more sensitive to it than others are and ford makes some real weak ones. It will make a difference over time. It's not like we are trying to predict the future, it has already ruined one trans and the dealer has indicated this as the cause and I agree with them. Increasing the gear ratio causes the tranny to work harder and run hotter. It's certainly not ideal and should be avoided in the future.
Was this
answer
helpful?
Yes
No
Saturday, May 28th, 2011 AT 2:11 AM
Tiny
CJ MEDEVAC
  • MECHANIC
  • 11,004 POSTS
Here you go!

A solution to your problem!

The right size!

I did not "Browse" a long time, but this was the least expensive I found in 10 minutes! I know you can do better, with a little more time!

Got my Tires on Ebay, Installed/ Balanced them myself, on my buddy's manual changer.

Even if you had a tire shop do it, You would still save $$$!

The Medic
Images (Click to make bigger)
Thumb
Thumb
Thumb
Thumb
Thumb
Thumb
Was this
answer
helpful?
Yes
No
Tuesday, May 31st, 2011 AT 2:56 AM

Please login or register to post a reply.

Related Tire Size Content